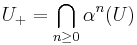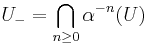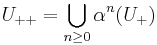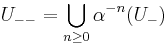Totally disconnected group

In mathematics, a totally disconnected group is a topological group that is totally disconnected. Such topological groups are necessarily Hausdorff.

Interest centres on locally compact totally disconnected groups (variously referred to as groups of td-type,^[1] locally profinite groups,^[2] t.d. groups^[3]). The compact case has been heavily studied – these are the profinite groups – but for a long time not much was known about the general case. A theorem of van Dantzig from the 1930s, stating that every such group contains a compact open subgroup, was all that was known. Then groundbreaking work on this subject was done in 1994, when George Willis showed that every locally compact totally disconnected group contains a so-called tidy subgroup and a special function on its automorphisms, the scale function.

1 Locally compact case
2 Notes
3 References

Locally compact case

In a locally compact, totally disconnected group, every neighbourhood of the identity contains a compact open subgroup. Conversely, if a group is such that the identity has a neighbourhood basis consisting of compact open subgroups, then it is locally compact and totally disconnected.^[2]

Tidy subgroups

Let G be a locally compact, totally disconnected group, U a compact open subgroup of G and $\alpha$ a continuous automorphism of G.

Define:

$U_{%2B}=\bigcap_{n\ge 0}\alpha^n(U)$

$U_{-}=\bigcap_{n\ge 0}\alpha^{-n}(U)$

$U_{%2B%2B}=\bigcup_{n\ge 0}\alpha^n(U_{%2B})$

$U_{--}=\bigcup_{n\ge 0}\alpha^{-n}(U_{-})$

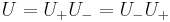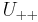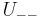U is said to be tidy for $\alpha$ if and only if $U=U_{%2B}U_{-}=U_{-}U_{%2B}$ and $U_{%2B%2B}$ and $U_{--}$ are closed.

The scale function

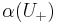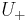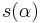The index of $\alpha(U_{%2B})$ in $U_{%2B}$ is shown to be finite and independent of the U which is tidy for $\alpha$ . Define the scale function $s(\alpha)$ as this index. Restriction to inner automorphisms gives a function on G with interesting properties. These are in particular:
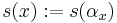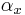Define the function $s$ on G by $s(x):=s(\alpha_{x})$ , where $\alpha_{x}$ is the inner automorphism of $x$ on G.

$s$ is continuous.
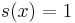$s(x)=1$ , whenever x in G is a compact element.
$s(x^n)=s(x)^n$ for every integer $n$ .
The modular function on G is given by 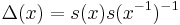$\Delta(x)=s(x)s(x^{-1})^{-1}$ .

Calculations and applications

The scale function was used to prove a conjecture by Hofmann and Mukherja and has been explicitly calculated for p-adic Lie groups and linear groups over local skew fields by Helge Glöckner.

Notes

^ Cartier 1979, §1.1
^ ^a ^b Bushnell & Henniart 2006, §1.1
^ Borel & Wallach 2000, Chapter X

References

Borel, Armand; Wallach, Nolan (2000), Continuous cohomology, discrete subgroups, and representations of reductive groups, Mathematical surveys and monographs, 67 (Second ed.), Providence, Rhode Island: American Mathematical Society, ISBN 978-0-821-80851-1, MR 1721403
Bushnell, Colin J.; Henniart, Guy, The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Berlin, New York: Springer-Verlag, doi:10.1007/3-540-31511-X, ISBN 978-3-540-31486-8, MR 2234120 | year=2006 | volume=335}}
Cartier, Pierre (1979), "Representations of $\mathfrak{p}$ -adic groups: a survey", in Borel, Armand; Casselman, William, Automorphic Forms, Representations, and L-Functions, Proceedings of Symposia in Pure Mathematics, 33, Part 1, Providence, Rhode Island: American Mathematical Society, pp. 111–155, ISBN 978-0-821-81435-2, MR 0546593, http://www.ams.org/online_bks/pspum331/pspum331-ptI-7.pdf
G.A. Willis - The structure of totally disconnected, locally compact groups, Mathematische Annalen 300, 341-363 (1994)